LE GEOMETRIE NON EUCLIDEE

La geometria è una parte della matematica che studia le proprietà delle figure, o più precisamente le relazioni fra punti, rette, piani e spazi. Sviluppatasi inizialmente su basi empiriche si è poi evoluta a livello teorico. Tra coloro che maggiormente contribuirono allo sviluppo della geometria classica ci fu Euclide. La sua geometria è costruita su 23 definizioni(riguardanti enti geometrici primitivi: punto, linea ecc...), 5 assiomi(o postulati) e 5 nozioni comuni(enunciati di carattere generale chiaramente evidenti). Ogni teorema viene da Euclide dimostrato per mezzo di successive deduzioni derivanti dagli assiomi e dai teoremi dimostrati in precedenza.

I cinque postulati sono:

1) da qualsiasi punto si può condurre una retta ad ogni altro punto;

2)ogni segmento si può prolungare continuamente per dritto;

3)con ogni centro e ogni distanza si può descrivere una circonferenza;

4)tutti gli angoli retti sono uguali fra loro;

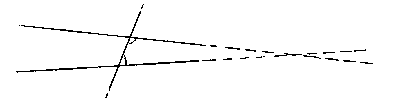
5)se una retta, incontrandone altre due, forma gli angoli interni da una stessa parte minori di

due retti, le due rette prolungate all’infinito si incontrano dalla parte in cui sono i due angoli

minori di due retti.

  La geometria di Euclide costituì per molti secoli il modello di ogni teoria ipotetico-deduttiva e ogni analisi critica di essa si ridusse ad un esame attento dei suoi postulati in particolare del 5° . I primi critici evidenziarono così il "neo" della sistemazione euclidea rappresentato dall’assunzione del 5° postulato e con i loro tentativi portarono alla scoperta delle geometrie non-euclidee nei primi decenni del XIX sec. d.C. I vari tentavi si orientarono su tre fronti differenti :

1) assunzione di una definizione di parallele diversa da quella di Euclide;

2)sostituzione del 5° postulato con una proposizione più intuitiva;

3)dimostrazione del postulato come teorema deducendolo dagli altri postulati. Tra i primi ad intraprendere queste strade vi fu Proclo (410-485) che prima di presentare una propria soluzione si riferisce ai tentativi di alcuni suoi predecessori come ad esempio Posidonio (I sec. a.C.). con la sua soluzione (due rette sono parallele quando complanari ed equidistanti), però non risolve affatto la questione dato che per essere dimostrata necessita del 5° postulato euclideo.

Altri tentativi furono messi in pratica da commentatori arabi che introdussero procedimenti dimostrativi e ipotesi talora geniali. I veri e propri precursori delle geometrie non euclidee iniziano la loro opera a partire dal XVIII sec. d.C.

Saccheri cerca di risolvere la questione del postulato delle parallele con originalità e rigore. Egli applica il metodo di ragionamento già elaborato nella sua precedente opera per dimostrare che il 5° postulato è una conseguenza logica degli altri quattro. Il suo scopo è quello di ricavare dalla negazione del postulato delle parallele tutte le conseguenze logiche fino ad incontrare una incompatibile con uno degli altri quattro postulati di Euclide. Saccheri è il primo ad esaminare tutte le possibilità di un’ eventuale negazione del 5° assioma e perciò può essere considerato il precursore di entrambe le geometrie non-euclidee: quella ellittica e quella iperbolica.

Anche Lambert ha una figura di spicco in questo periodo. La sua opera è composta di tre parti:

1) la prima discute la possibilità di ricavare il quinto dagli altri 4 postulati;

2) la seconda tenta di frammentare il postulato in proposizioni semplici che richiedono una dimostrazione;

3) la terza infine è una ricerca analoga a quella di Saccheri. Legendre tenta di dimostrare il quinto postulato ricavandolo dalla proposizione, la somma degli angoli interni di un triangolo è uguale a due angoli retti, che deve dimostrare a sua volta. Una delle geometrie non-euclidee è quella iperbolica scoperta ufficialmente da Lobacevskij e Bolyai.

Il sistema è basato sull’ipotesi dell’angolo acuto di Saccheri o di Lambert (per un punto esterno ad una retta si possono condurre due parallele alla retta data). Quella invece fondata sull’angolo ottuso che comporta la non esistenza di rette parallele ha portato allo sviluppo di un secondo sistema detto ellittico.

  Nel sistema iperbolico la distanza fra due rette intersecantesi aumenta indefinitamente mentre quella tra due parallele diminuisce e tende a zero nella direzione di parallelismo aumentando nella direzione opposta.

In questo sistema due rette possono:

1)intersecarsi secondo un angolo diverso da 0 ma hanno perpendicolare comune.

2)non intersecarsi e ammettere una perpendicolare comune, cioè sono divergenti in entrambe

le direzioni;

3)essere parallele, cioè possono formare all’infinito un angolo nullo ammettendo però una perpendicolare comune. Un altro concetto fondamentale nella geometria iperbolica è quello di Oriciclo che può essere illustrato come segue:

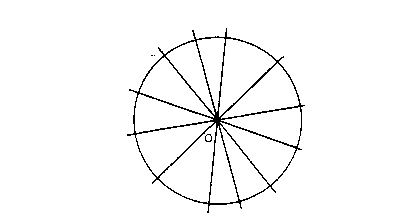  Si consideri una circonferenza di centro O di tipo euclideo, ogni raggio è perpendicolare alla circonferenza stessa. Supponendo di aumentare indefinitamente il suo raggio le rette del fascio (raggi) diventano parallele e la circonferenza assume una forma limite che nella geometria euclidea è una retta.

Nel sistema iperbolico invece tale elemento è una curva uniforme detta appunto oriciclo e che resta definita come la traiettoria ortogonale di un fascio di rette parallele. Questo concetto può essere anche esteso dal piano allo spazio (orisfera). Nella geometria iperbolica la somma degli angoli interni di un triangolo è minore di due retti.

L’ideatore dell’altra geometria non-euclidea(quella ellittica ) è Bernard Riemann (

1826-66). La scoperta di questo sistema è avvenuta nella seconda metà dell’800. Il sistema di geometria ellittica si basa sull’ipotesi che lo spazio sia finito, in particolare ciò fa riferimento alla retta che a differenza dei casi euclideo e iperbolico è chiusa e finita.

Nella geometria riemanniana, per evitare contraddizioni, bisogna variare ulteriormente i postulati euclidei. Ad esempio nel sistema ellittico si postula che due rette possano racchiudere un’area e può esistere anche più di una retta che unisce due punti differenti. Dato che il postulato delle parallele di Euclide ha un ruolo molto importante nella dimostrazione del teorema riguardante la somma degli angoli la sua negazione ha portato ad esso una variazione. Secondo Riemann una retta può essere disegnata come il cerchio massimo di una sfera, poiché la sua geometria è a quattro dimensioni, quindi per un punto esterno non passerà mai una parallela (due circonferenze massime si incontrano sempre due volte). Nella geometria ellittica l’angolo esterno di un triangolo è minore di ciascuno degli angoli interni non adiacenti al contrario di quanto si afferma nella geometria euclidea. Riemann affermava che la somma degli angoli di un triangolo fosse maggiore di 180° dato che per lui un triangolo, detto sferico, è costituito dagli archi di tre cerchi massimi. Infine anche nella geometria ellittica è possibile definire delle "curve equidistanti" dette parallele di Clifford.

I sistemi geometrici non-euclidei appaiono così costruiti, "consistenti", cioè privi di contraddizioni. Quindi si è posto il problema di dimostrare realmente la loro consistenza. I metodi per fare ciò possono essere due:

1)dimostrare che è impossibile ottenere una proposizione contraddittoria; 2)confrontare il sistema in questione con un altro esente da contraddizione; ciò consiste nel rappresentare i concetti dell’uno in quelli del secondo e vedere se hanno ugualmente significato.

Optando per il secondo metodo si è deciso di confrontare i sistemi non euclideei con quello euclideo. Gli studiosi che lavorarono in questo progetto ottennero il modello della geometria iperbolica ( per porzioni limitate del piano) rappresentando gli essenziali elementi non euclidei, come il punto e la retta sulla pseudosfera, una superficie euclidea avente curvatura costante e negativa.

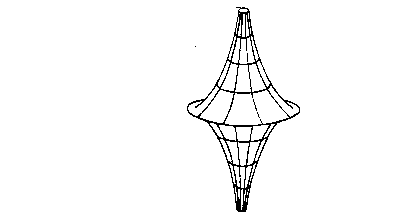
Esaminando sul piano euclideo una circonferenza può essere stabilito il seguente rapporto tra elementi euclidei e non euclidei.

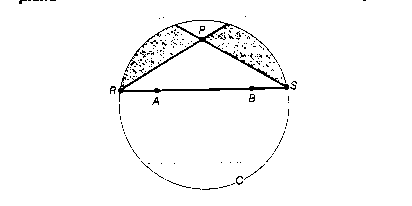
Si vede che in questo modello esistono due parallele alla retta RS (PS e PR)

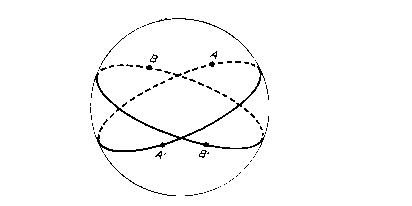  Anche in questo caso valgono gli assiomi euclidei tranne il 2° e il 5° perchè non si hanno rette parallele.

Le geometrie non-euclidee hanno contribuito a una migliore comprensione del metodo assiomatico e del suo significato per la scienza, migliore di quello che si sarebbe potuto raggiungere se i matematici, i fisici e gli astronomi si sentissero ancora obbligati ad accettare la geometria euclidea quale rivelazione di una verità geometrica finale.